Mar 20 2015
Titius-Bode Law and Exoplanets
 A recent Washington Post headline reads: Most stars in the galaxy have planets in the habitable zone, according to new research. Some version of this headline was attached to every mainstream media reporting on this story. Not just the headlines were this hyped – most of the time the reporting presented this new research as if this is an accepted conclusion.
A recent Washington Post headline reads: Most stars in the galaxy have planets in the habitable zone, according to new research. Some version of this headline was attached to every mainstream media reporting on this story. Not just the headlines were this hyped – most of the time the reporting presented this new research as if this is an accepted conclusion.
I have been following our exoplanet explorations since they began. Like many astronomy enthusiasts, I am particular interested in a few questions – how many planets do stars have on average, what are the typical arrangements of those planets, how typical or atypical is our own system, and how many earth-like planets are out there? We are starting to get a good idea of how many exoplanets are out there – most stars likely have multiple planets.
The other questions are still open at this time. While we are gathering more and more data points, with hundreds of systems now known to have planets, and currently 1,821 confirmed exoplanets. There are a couple thousand more possible exoplanets awaiting confirmation.
This may sound like a lot, but it really isn’t nearly enough data points to answer the remaining questions above. One problem is that we don’t have a thorough survey of each system. We are finding planets that are the easiest to find – those close to their parent stars, and larger planets. Small planets far from their stars would be almost impossible to find given current methods. They would not have a significant gravitational effect on their parent star, and even if they happened to transit their star they would probably have an undetectable effect on the light from that star. Also, with periods of hundreds of years, it would take hundreds of years to confirm them by the transit method.
Therefore our data on the planetary composition of other solar systems is incomplete and biased. We just don’t have enough data to draw many conclusions about the composition of planetary systems. We can answer some questions, like how many systems have hot Jupiters, jovian planets close to their stars?
Fortunately, we can detect earth-sized planets in the habitable zone of their stars because for many stars that puts them close enough to detect and confirm using the transit method.
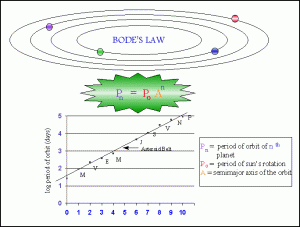
The researchers in the current paper, the one grabbing exciting headlines, used a theoretical method to predict the composition of planetary systems in which we have detected between three and six planets. They then applied the Titius-Bode law to predict where other planets likely reside. One problem with this approach is that the T-B law is not really a law. It is not generally accepted as having genuine predictive value. At the very least it should be considered controversial.
Titius first noticed that the planets in our system are spaced out in a regular pattern, and Bode worked out the math in 1778. If you take the series 0, 3, 6, 12, 24, 48, 96, 192. 384 (after the three you simply double the preceding number), then add four to each number and divide by ten, you get a very good approximation of the distance in astronomical units of the planets in our solar system from the sun. According to this sequence, there should be a planet at 2.8 AU, which corresponds to the asteroid belt and the dwarf planet, Ceres.
Does this mathematical relationship reflect underlying physics, perhaps something to do with probability of stable orbits, or gravitational fields, or is it just numerology? Perhaps it’s a bit of both – orbits might have a tendency to be spaced out in a certain way because if they were too close together they might gravitationally disrupt each other’s orbits, but the precise mathematical relationship is just a coincidence and not a “law” of any kind.
The hallmark of science is not the ability to explain existing observations, but the ability to predict future observations. How well does the T-B law predict, for example, the orbits of moons that were not discovered until later? For those large planets that have moons which likely formed with the planets (as opposed to captured later) they do appear to have a regular spacing, but in a non-Bode pattern. So the regular spacing part seems to hold up so far as a reasonable rule of thumb, but there does not appear to be a precise mathematical relationship. This, of course, has led many to try to work out variations on Bode’s math to derive a more general rule. One example being Dermott’s law. Again, none of these are generally accepted, they are mostly dismissed as numerology and popular fascination with working out the math seems to be an annoyance to journal editors and serious astronomers.
Now that we are in the age of exoplanet discovery, the T-B law has a new life and researchers who are so inclined have new sets of data to apply their favorite version of Bode’s math. This is what the current researchers are doing. They claim that of the 151 systems they looked at a “generalized version” of Bode’s law holds up in 124 of them. They then calculate where additional planets should be in those systems. That is how they predict that most systems will have 1-3 planets in the habitable zone.
From reading the headlines one might assume that scientists were counting confirmed exoplanets, but no, they were counting theoretical exoplanets. Further, the application of the “generalized version” of Bode’s law makes me wonder how much wiggle room this allowed. That is a common criticism of the T-B concept – that in any system where planets are simply spaced out so as not to bump into each other, you can force fit some mathematical series if you give yourself some wiggle room.
The best thing about this study, however, is that it makes specific predictions about where new exoplanets may be discovered. If their generalized version of T-B is found to have genuine predictive value, that would make it more than wild speculation. However, the devil will be in the details – how close will future exoplanets have to be to their predicted location, and how many of them are needed before the idea is considered confirmed? Again there is the potential for wiggle room, allowing the actual data, almost no matter what it is, to fit the theory.
What is most disappointing, as usual, is that the mainstream media generally failed to properly report this story. This is a speculative paper, and honestly is not even worth reporting to the public as a news item. The bottom line, expressed in the headline, is highly misleading, and is not a finding of this paper. This type of speculative research should be relegated to the technical literature, or at best popular science magazines where the nerdy details can be explained thoroughly and the paper put in its proper context.






