Back in the early days of my skeptical career I attended a skeptical conference hosted by CSI (then CSICOP). One panel stuck out, and I still remember some details more than two decades later. This was a panel on extrasensory perception (ESP). The proponent on the panel argued that the research showing that ESP is real shows as much of an effect as the research showing that aspirin prevents strokes. Therefore if we accept one, we should accept the other. Even my nascent skepticism was able to detect that this argument did not hold water, but now I understand why in far greater detail. There are many problems with the claim (such as the quality of the research and the overall pattern of results) but I want to focus on one – the role of prior probability.

This is often a sticking point, even among mainstream scientists and clinicians, I think because of the inherent human lack of intuition for statistics. Most scientists are not statisticians, and are prone to making subtle but important statistical mistakes if they don’t have proper consultation when doing their research. In fact, there is an entire movement within mainstream medicine that, in my opinion, is the result of large scale naivete regarding statistics – evidence-based medicine (EBM).

EBM focuses on clinical research to answer questions about whether or not a treatment works. Conceptually EBM explicitly does not consider prior probability – it only looks at the results of clinical trials directly asking the question of whether or not the treatment is effective. While this may seem to make sense, it really doesn’t.

Let me explain.

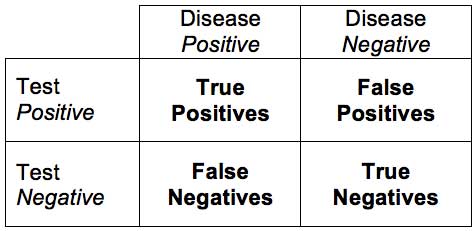
Let’s say we have a test for the presence of a disease (I am going to use fake examples so I can just make up numbers to illustrate my point, but this applies to real examples just as well). Let’s call the test a scanomatic, which can detect the presence of groot disease. If the scanomatic has a 95% sensitivity and 95% specificity for detecting groot, what is the probability that someone has groot if they have a positive test? For review, sensitivity is the percent of people who have the disease who will test positive (the true positive rate). Specificity is the percentage of people who do not have the disease who will test negative (the true negative rate). So what’s the answer?

Interestingly, not only will most people get the answer to this question wrong, most doctors will get the answer wrong. Again – this is not intuitive. People basically naturally suck at statistics.

The answer is – you don’t know. You are missing a critical piece of information, which is something people tend to ignore – the base rate. How many people in the population you are testing have groot? In other words – what is the pre-test or prior probability of the condition? Let’s say that 1% of the population have groot (this would make it a common disease). That means that out of 100 people, 1 person has the disease, and 0.95 will test positive (true positive with 95% sensitivity). This also means that 99 people will not have the disease and 4.95 will test false positive (with a 95% specificity). This means that out of everyone that tests positive (4.95+0.95) only 16% will actually have groot. So the predictive value of a positive scanomatic test is only 16%, even with a very sensitive and specific test.

This number is much lower than most people intuitively guess. But even more important – most people do not even consider the base rate when trying to come up with the answer. They ignore prior probability – just like EBM.

So let’s apply this same logic to a scientific study. If a study finds a difference between placebo and treatment with a p-value of 0.05, what is the probability that the treatment works? Again, most people (even professionals) will wrongly say 95%. In reality the answer is – you don’t know. You need to know what the prior probability of the treatment working is, just like you need to know the base rate in the population of groot disease. Taking into consideration the prior probability is what I call science-based medicine (there is a lot more to it, but that is the core).

To illustrate how important prior probability can be, let’s assume that the rate of groot in the population is 1/1,000. Then the predictive value of our positive scanomatic drops to 1.7%. What if it is 1/10,000? Then the predictive value is 0.02%. As you can see, as the prior probability decreases, the chance that a treatment actually works even with a positive clinical trial with a p-value of 0.05 rapidly approaches zero. This is exactly why we don’t screen populations with a very low incidence of the target disease. At some point the true positives become negligible compared to the false positives.

This is partly why it is absurd to compare p-values with ESP and aspirin prophylaxis. The prior probabilities are completely different.

All of this is also partly why there is an increasing movement in the scientific community away from relying heavily on p-values alone. Doing so encourages this very common statistical error. It is far better to take a more thorough look at the data – including effect sizes, reproducibility, confidence intervals – and to combine everything into what is known as a Bayesian approach. The Bayesian approach is essentially to look at the prior probability, then add the new data and calculate a posterior probability. You can’t look at the new data in a vacuum, you need to put it into the context of prior probability.

How do we know what the prior probability of a new scientific hypothesis is? We don’t. There is no gold standard. It’s not like a disease where we have data on the incidence of that disease in the target population. Generally we are researching questions we don’t know the answer to. So we have to guess based upon our best judgement, which includes looking at all scientific evidence, basic and applied, and coming up with a reasonable estimate. Of course this introduces a layer of bias, as all judgement calls do. But we can at least make broad statements about high and low probability. How much existing evidence contradicts the new hypothesis? Would it break any laws of physics? Does it require the introduction of entirely new and unknown phenomena? Is there a mechanism that is at least physically plausible? What does the preliminary evidence say?

We can also look at the scientific literature and the history of science and ask sweeping questions – how many new scientific hypotheses turn out to be true? How many published studies come to the correct conclusion when evaluated later, after decades of hindsight when we pretty much know the answer? How new vs mature is this field of study? Are we building on a solid foundation, or groping in the dark? How objective vs subjective are the things were are trying to measure?

There is no shortcut to a reasonable answer, you need to do a thorough and highly technical analysis with specific knowledge of the subject area. Basically, you need to be an expert. Or, you can know enough to figure out what the consensus of expert opinion is, how valid the particular area of inquiry is, and how solid the foundation is.

The short answer to the questions above is this – most new ideas in science turn out to be wrong, and most published studies come to the wrong conclusion, with a huge bias toward false positives. There is also publication bias and citation bias that further reinforce this positive bias. We can add to that p-hacking and other failures of rigorous research design and execution (this would be analogous to a technical failure in the scanomatic). Further, all research has limited resources and abilities, and therefore involves compromise and trade-offs. There are also different ways to approach the same question, which may yield different answers.

We need to put all of this together into a holistic assessment of whether or not we think something is likely to be real. It’s a mess. Fortunately, eventually we can grind our way to a highly reliable answer. When a hypothesis survives multiple attempts at proving it wrong, and is supported by multiple independent lines of evidence, is able to make highly accurate predictions, and the results hold up to independent replication over a long time, we gain more and more confidence in the conclusion.

The notion that we can look myopically only at the results of clinical trials and have a good idea if something works or a hypothesis is true simply doesn’t hold water. In practice, even among those professing to practice EBM, that is not what happens. Experts do take a more holistic approach to the evidence, and use an EBM analysis as just one type of evidence. But the limited EBM approach, while it has had some positive effects on the science of medicine (increasing the standards of clinical evidence), has also had some negative effects, in my opinion. It has opened the door to highly implausible treatments and ideas. If you are promoting a treatment that has a very low prior probability, then you are happy to ignore this probability and just look at one type of evidence (one that happens to also be very susceptible to p-hacking).

If we consider homeopathy, for example, it is reasonable to consider that there is no known mechanism by which homeopathy can possibly work. The claims break the known laws of physics. We might also consider that 200 years of study has failed to show any mechanism, and the predictions implied by homeopathy have been refuted by 200 years of subsequent scientific advance. It’s reasonable to assign a low prior probability to the notion that homeopathy works, which means limited clinical evidence with a p-value of 0.05 (or even lower) does not significantly affect the posterior probability – it still approaches zero. We would need a clinical home-run, a clear clinical effect that is easily reproducible. Homeopathy does not have that.

In fact, even if we take an EBM approach to homeopathy, the clinical evidence is negative. It doesn’t even make that low bar, let alone the higher bar of SBM.

The lesson here is – always consider the prior probability, the pre-test probability, or the base rate when considering new evidence. Prior probability matters.