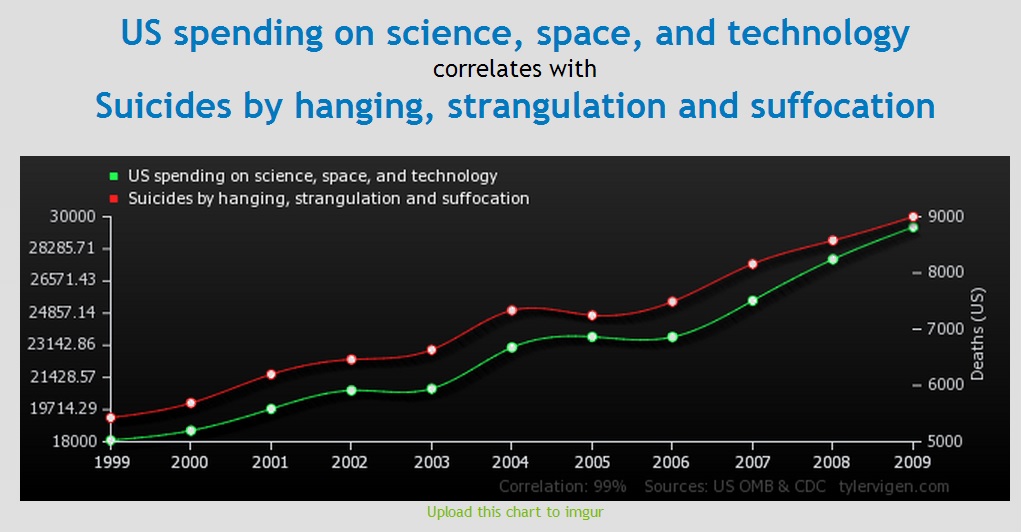
Every skeptic’s new favorite website is Spurious Correlations. The site is brilliant – it mines multiple data sets (such as causes of death, consumption of various products, divorce rates by state, etc.) and then tries to find correlations between different variables. The results are often hilarious.

The point of this exercise is to demonstrate that correlation does not necessarily equal causation. Often it is more effective to demonstrate a principle than simply to explain it. By showing impressive looking graphical correlations between phenomena that are clearly not related (at least proposing a causal connection superficially seems absurd.), it drives home the point that correlation is not enough to conclude causation.

I think most people can intuitively understand that funding on science, space, and technology is unlikely to have a meaningful causal connection to suicide by hanging, strangulation, or suffocation.

Yet – look at those curves. If a similar graph were shown with two variables that might be causally connected, that would seem very compelling.

There are a couple of points about this I want to explore a bit further. First is the important caveat that, while correlation is not necessarily causation, sometimes it is. Two variables that are causally related would correlate. I dislike the oversimplification that is sometimes presented: “correlation is not causation.” But it can be.

The second point is a statistical one. The important deeper lesson here is the power of data mining. Humans are great at sifting through lots of data and finding apparent patterns. In fact we have a huge bias toward false positives in this regard – we find patterns that are not really there but are just statistical flukes or complete illusions.

Correlations, however, seem compelling to us. If we dream about a friend we haven’t seen in 20 years then they call us the next day, that correlation seems uncanny, and we hunt for a cause. We aren’t even aware of the fact that we are sifting a massive set of data for this apparently stunning correlation – everything that happens to us throughout our day. The opportunities for chance correlations are huge, and it is not surprising that we find some.

This website is doing essentially the same thing, just with graphical data. It is sifting through large numbers of graphs, and finding spurious correlations.

This sometimes happens with published data as well, even if it is not completely apparent. Scientists may look through data for many possible correlations before finding one. They may or may not publish all the possible correlations they looked for, and when they don’t, the one that they found will be made to seem much more impressive than it is.

If correlations are questionable but not useless, how should we consider them? Finding correlations is a useful way to generate hypotheses, but is a very weak method for testing hypotheses. In other words, when an apparent correlation is found it should be considered a hypothesis, not a conclusion.

Before we engage in too much speculation about cause, it is better to confirm the correlation first. One way to do this is to look specifically for that one correlation in a fresh set of data. The initial observation of the correlation likely came out of many possible observed correlations, many more than may naively seem to be the case. We can control for this hidden multiple comparisons by looking only for the one apparent correlation.

It is critical, however, that a completely new and independent set of data be used. If you include the old data then you can be bringing forward the chance correlation.

Once the correlation is confirmed as probably real, the next step is to explore possible causal relationships. In general, if A correlates with B then it is possible that A causes B, B causes A, or both A and B are related to a third factor, C. This analysis should be guided by prior plausibility.

For example, many things correlate with population. So any area with a growing population will also see correlations between any factors that also tend to grow with population.

There are two basic ways to confirm a specific causal relationship – observational and experimental. The most reliable type of data is experimental, because you can control for variables. You can see if increasing A increases B, or the other way around.

It is not always possible to do controlled experiments, however. In such cases further observational data is useful. Each possible causal connection may make different predictions about further correlations, and these can be used to test the various causal hypotheses.

Observational data is always suspect, because there can be an unknown variable that is not being controlled for in the data. For example, there is some research showing a correlation between violence in video games and aggression. A recent study, however, showed that aggression actually correlates with frustration from playing difficult games, and not their level of violence. (I am not saying this is the final word – just that new research has exposed another confounding variable not accounted for in prior research.)

Conclusion

Correlations are an important part of scientific research. We also use apparent correlations in our everyday life to reach conclusions about cause and effect.

Having a nuanced understanding of the complex relationship between correlation and causation is very useful, and essential for any researcher or just anyone trying to make sense of published research.

The spurious correlations website drives home what is often the first lesson that we must internalize – correlation is not necessarily causation.

Neither, however, can we dismiss correlations, because sometimes they are real and are a clue to causation. Further thoughtful research is needed, however, to confirm that an apparent correlation is real, and then to explore the true implications of real correlations.